各方面研究表明,对于风荷载的作用,即使是高柔结构,在绝大多数情况下也只需考虑基本振型。结构的风振时程本身也是一个平稳随机过程,对其结构反应的频谱特性分析可知,与主体结构本身基本振型周期及风脉动卓越周期相对应的这两个分量最高,因此可以用其中较高的一个频谱,一般即为基频

,近似地计算结构反应的上限值。设主体结构在风荷载作用下,以基本频率

发生简谐振动,如果取图(1)b坐标系统,则幕墙构件各点的位移及加速度可分别写成下面函数形式:
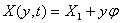
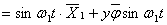
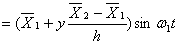 (1)
(1)
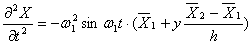 (2)
(2)
式中,
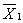
、
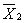
分别为构件下、上两点在主体结构按基频振动时的最大位移幅值,可由各层最大风振位移求得,近似地对应于结构自由振动第一振型的振动向量或振型函数中的相应数值。主体结构的风振并不是简谱振动,但上式可表达最大反应的上限值。
对于自身尺度小、质量分布小、相对
刚度大的幕墙构件,它们对于主体结构的相对位移振动,其频率与主体结构的输入频率即主体基频相比高出甚多,因此不容易发生共振;与风的脉动频率相差更远(风的卓越周期一般在4秒以上),因此幕墙构件直接的风振效应也很微弱。正如规范规定的总体高度小于30m的结构物不必考虑风振效应一样,对它们的自身强度和与主体结构连结的验算,可以认为它们是相对于主体结构的刚体而不计风振系数。即使处于较高位置的构件,风载值虽然比低处有所增高,但研究表明,反映最大瞬时风速的湍流强度值随位置增高而减小,这样脉动效应仍不大。
在跟随主体结构前、后摆过程中,幕墙构件运动到平衡位置时速度最大,这会造成构件与气流相对速度的增加或减小;根据对一般工民建结构物的基频和振幅的常见范围的分析,上述摆引起的风压改变极小,更何况速度最大时与位移最大(内力亦最大)时不同时发生,困此不必加以考虑。
下面求竖向
简支梁构件如
铝合金玻璃幕墙立柱的最大风振内力。设构件单位长度质量分布
集度为
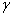
,见图(1)b,则沿竖向任一点根据d′Alembert原理,该点惯性力微分表达式:

将式(2)代入上式,可得最大的微分惯性力的表达式为:
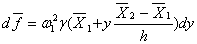
也即就是惯性力的幅值沿简支梁的分布为梯形
线荷载,(2)图,其中:
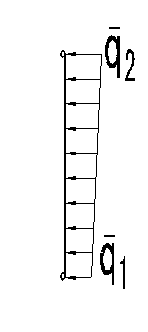
图(2)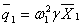
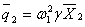
 上一页123下一页
上一页123下一页
