根据计算结果,张弦梁上弦杆最大应力比为0.445,其它杆件最大为0.828 ;φ5x85的索最大破断力为200 0kN ,按规范要求索抗立
分项系数取2.0 ,则索应力比为843/(2000/2=0.843,φ5x85索最大破断力为2782k N,则索应力比为1121/(2782/2)= 0.806 ,均满足规范要求。
(4) 抗震分析采用振型分解反应谱法考虑竖向地震作用,计算表明地震作用与其它荷载
作用效应组合不起控制作用,计算所得结构前三阶振型如下:
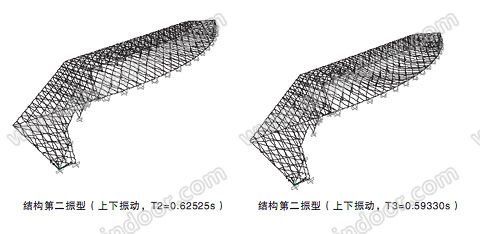
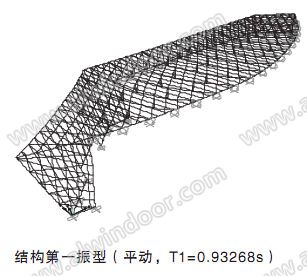
(5) 结构屈曲分析:
1、 首先对结构进行特征值屈曲分析
通过线性特征值屈曲分析,可以得到理论上的屈曲稳定特征值系数和屈曲模态。屈曲稳定系数如下表1,第一阶屈曲模态见图3,由分析结构表明结构首先出现失稳表现为屋面结构弯曲失稳。

2、 非线性屈曲分析结果:
采用ANSYS进行非线性屈曲分析,根据规范
[4]要求,以跨度的1/300作为该结构的最大缺陷值,考虑结构几何非线性的影响,材料本构关系采用理想弹塑性模型,对应荷载工况1.0恒+1.0活得到结构的荷载位移曲线,计算结过得到的失稳时的临界荷载约为实际荷载的5.5倍左右,大于规范[4]要求,说明结构整体性良好。
4 主要节点设计
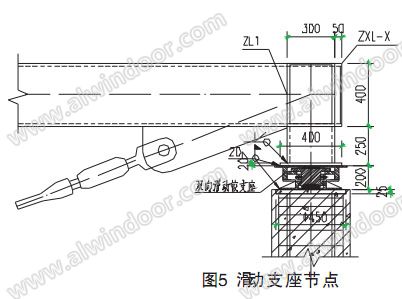
4.1支座及节点:
本工程支座主要有两种连接形式:第一种为与地面和裙房屋顶的固定连接支座具体详见图4 ;第二种为与主塔楼连接的水平滑动支座,具体详见图5此 支座主要考虑屋面张弦梁结构的预应力自平衡和减少主塔楼在水平地震力作用下对采光顶的影响。
4.2撑杆与上弦杆、拉索连接节点:
张弦梁结构下弦拉索与撑杆之间必须固定,其节点构造应保证将索夹紧,不能滑动。本工程采用由2个实心半球组成的索球节点来扣紧下弦拉索,如图6所 示。下弦索平面外没有支撑,因此撑杆与上弦构件的节点通常设计为平面内可以转动,平面外限制转动的节点构造形式[5] ,详见图7所示。

5 结束语
(1)张弦梁结构一般跨度较大
屋面自重轻,在风吸力较大的情况下可能导致下部预应力索拉力丧失,结构是失稳,设计时尤其要注意,必要时须加大结构自重或增加反向稳定索。
(2)确定索的初始预应力时
既要考虑结构荷载状态下张弦梁的安全,又要考虑结构初始态的稳定。
(3)为保证撑杆与上弦杆和下部索为理想铰接
上部采用销钉式连接铰,下部采用索球铰。
考虑到撑杆在张弦梁外必须具有刚度,因此上部铰仅为面内铰,面外须具有一定刚度。
参考文献
[1]张其林。玻璃幕墙结构[M] 济南:山东科学技术出版社,2006
[2]白 正仙,刘锡良,李义生。新型空间结构形式—张弦梁结构[J]。空间结构,2001(7)
[3] GB50009-2001 (2006年)建筑结构荷载规范[S]
[4] JGJ7-2010空间网格结构技术规程[S]
[5]董石麟,罗尧治,赵阳等。新型空间结构分析、 设计与施工[M] 北京:人民交通出版社,2006
 上一页123下一页
上一页123下一页
