3.试验结果及比较分析
3. 1试验曲线
将通过H P3502A测到的结果数据文件导入计算机,先经L IF软件转为D0 S文件,然后通过63T0SDF软件转换为SD F文件,最后用V正W DATA软件读取数据文件,根据每种工况的结果选取如图5所示的典型功率谱曲线(纵坐标S (f)为加速度功率谱有效值开方取对数处理后的值,横坐标f5为分析带宽频率)进行分析,提取索网的前三阶自振频率。
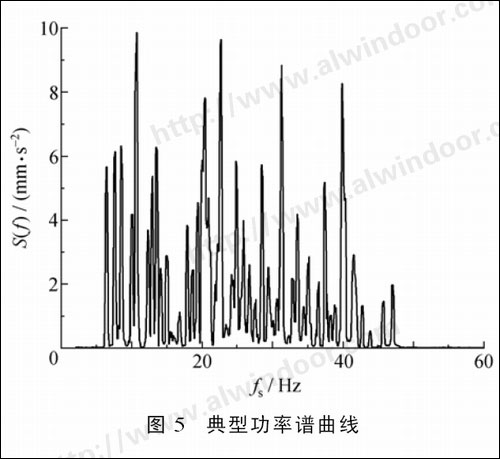
3.2自振特性的有限元分析
3.2- 1有限元模型
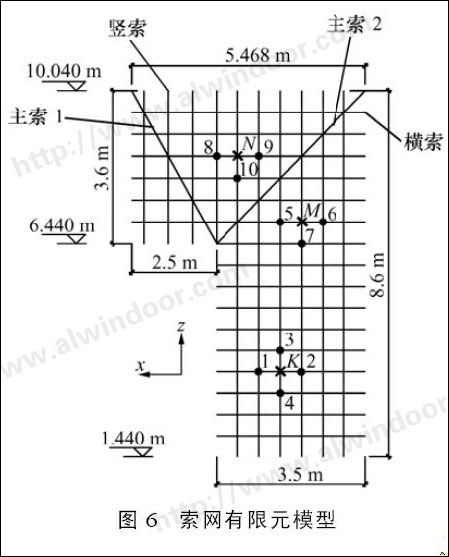
采用大型有限元分析计算软件ANSYS该单层索网进行模态分析。如图6所示,模型中主索及水平索采用了三维只拉单元linkl0单元,拉索则采用压link8单元。
为了便于简化计算,在采用ANSYS进行分析时,将索网与钢框架的连接视为固定端,只对索网进行分析。
3.22模态分析方法
柔性支承结构的刚度主要来源于杆件的初始预应力,而且索又是一种几何非线性极强的结构,因此,在模态分析时必须考虑这两方面的影响。
有限元分析中索的预应力靠设置初应变来实现。本文先根据试验各级预应力的实际加载情况,初设一组应变值,然后反复调节直至模型中各索的内力基本满足相应的试验实测值,将调好的这组应变值进行模态分析,主要步骤分为两步:
1))进行几何大变形的静力分析;
2)修正结点坐标,进行包含预应力影响的模态分析,读取自振频率及相应振型。
3.23有限元结果的提取
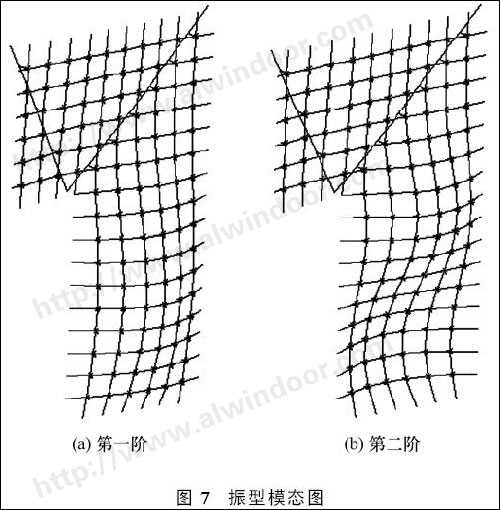
通过以上的有限元分析提取索网的自振频率及相应振型。图7为一级预应力时的前两阶振型模态图,前面所述的试验测点工况就是根据这些结果设
计的。
3.3索网自振频率的比较分析
图8该单层索网在各级预应力下频率试验和有限元计算结果的对比,其中横坐标F表示量纲一化的预应力,纵坐标fo为自振频率。
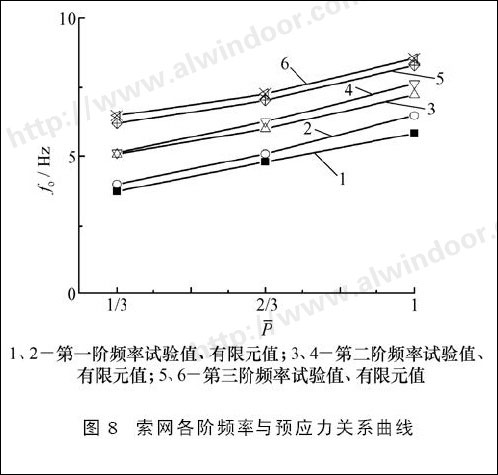
从图8中可以看出,理论与试验值的变化趋势很相似,试验值皆位于有限元计算结果以上,两者相差1. 01%~11. 330%,有限元计算中将索的支承视为固定未考虑支承钢架的影响,这也是两者存在差异的原因之一。
索网的频率基本随索内预应力的增加而呈弱非线性增长,并且随着频率阶次的增加,曲线形状逐渐由向上凹的趋势增加。这表明,尽管索网是几何大变形结构,但其频率随预应力的变化并未表现出明显的非线性性质;低阶频率随预应力的增长速度小于高阶频率的相应增长速度,即高阶频率与预应力之间的非线性性质更明显。
为了研究玻璃对索网刚度的影响,本文还测定了加玻璃后索网的频率,并与相应的有限元计算结果进行了对比,如表3所示,其中ft、ff分别为试验测得频率和有限元计算得到的频率值。
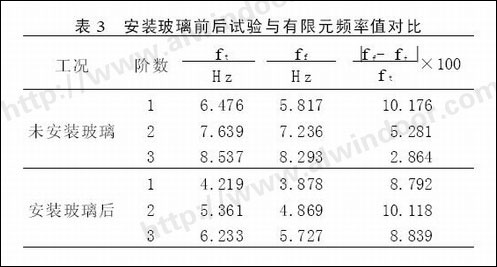
从表3可以看出如下规律。
1)安装玻璃前后索网频率的有限元计算值与试验值均比较接近,试验值比有限元计算值大2.86%一10. 18%,两者吻合较好,表明有限元模型比较符合实际结构。
由于采用ANSYS建模时对玻璃和索节点连接方式采用了3个方向的平动祸合,而实际结构玻璃与索网的连接采用了驳接式金属连接件,加上玻璃尺寸较小,连接件尺寸相对较大,对玻璃交点有较强的约束作用,因此实际结构玻璃参与的作用更大,对索网的刚度贡献更大,因此本文认为,这是试验值高于有限元计算结果的原因之一。
2)从试验值可以看出,安装玻璃后结构的各阶频率分别降低了34.852%、29.816%、26.988%,且降低幅度随模态阶数的递增而减小。这表明由于玻璃的存在,结构的刚度和质量同时增长,但玻璃质量的影响超过了其刚度的作用,导致整个结构的频率下降。本实验模型中玻璃之间未打玻璃胶,使玻璃不能发挥整体的协同作用,这也是其刚度效应不够显著的原因之一。
4.结论
1)索网低阶频率随预应力基本呈线性性质,它随预应力的增长速度大于高阶频率的相应增长速度,即高阶频率与预应力之间的非线性性质更明显。
2)安装玻璃后结构的频率迅速降低,这是由于玻璃的存在,结构的刚度和质量同时增长,但玻璃质量的影响超过了其刚度的作用,导致整个结构的频率下降。
3)有限元计算值与试验值均比较吻合,验证了理论计算模型的合理性。
与【】相关热点资讯:
【了解更多 “” 相关信息请访问
幕墙专区 】
 上一页123下一页
上一页123下一页
